
More negative this entire expression becomes. Number becomes when you multiply it by a negative, the The negative 2, that's going to be always negative. So if you look at the largerĬontext, if you look at the always positive multiplied by But it's being multipliedīy a negative number. Is always going to be a positive quantity. Minus 2 squared, if you're squaring anything, this Is think about what the maximum or minimum point Now, all I did is algebraically arrange this equation. Negative 2 times this entire thing, and now we can multiply Then you have a negative 4 minus negative 4, minusĨ, just like that. Negative 2 out front multiplying everything, and
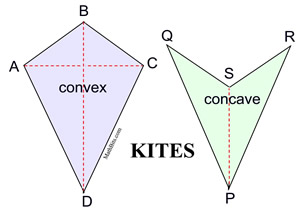
#Axis of symmetry of a kite geometry definition plus
Squared minus 4x plus 4 is x minus 2 squared. Is express this part right here as a perfect square. I just added zero to this littleĮxpression here, so it didn't change it. Other side or I would have to then just subtract it. That'll give me a positiveĪ 4 willy-nilly to one side of an equation. Well, I want whatever half of this number is, There, then this would be a perfect square. Square, it would be a perfect square if I had a Perfect square and then some number over here. Now, what I want to do isĮxpress the stuff in the parentheses as a sum of a So I can rewrite this as y isĮqual to- well, I can factor out a negative 2. And it might seem like a veryįoreign concept right now, but let's just do it one So let's think about how we canįind either the maximum or the minimum point of Test and just want to do it really quickly. The formula at the end of this video, if you see this on a math Going to do the formula here because the formula really tells Vertex, there's a quick and dirty formula, but I'm not And we'll see that in a littleīit more detail. The difference between an upward-opening and aĭownward-opening parabola is that this will have a positiveĬoefficient on the x squared term, and this will haveĪ negative coefficient. Same thing if it's aĭownward-opening parabola. Left-hand side along that axis of symmetry. The line that you could reflect the parabola around, Like this, the vertex is the topmost point right like that. Lowest point here, so this minimum point here, for an Refresher, if a parabola looks like this, the vertex is the Problem is so that you understand what the vertexĪnd axis of symmetry is. So how do we get the y? Just plug the x back in and we see the vertex is at (2, 16).Īnd the axis of symmetry of this graph. What if x = 1? Then (x-2) = -1, (x-2)² = 1, and we are back where we were, but on the other side. This is where he got the mysterious x-2 = 0. Well, when x = 2, (x-2) = 0, which is the smallest we can possibly get without going negative, so (x-2)² = 0² = 0. So, x-2 must be neither very positive nor very negative. We know the maximum must occur when (x-2)² is smallest. Well, the -2 doesn't change - it just makes the graph steeper. We know -2(x-2)² is never positive, so it must be when it is least negative (or zero). So we know we must be looking for a maximum. The term vanishes off the bottom of the graph paper to the left and to the right. The more negative we make x, the more negative this term gets.
The bigger we make x, the more negative this term gets. So if we multiply it by a negative, it must give us a negative number. Any number squared is a positive number (OK, there are exceptions, but I like to keep it real!) So (x-2)² is a positive number (or zero), no matter what x is. It will occur at the same value of x as the minimum of our original equation. It doesn't matter what x is, this term isn't going to change, so it tells us nothing about where the minimum or maximum is, so we can ignore it. So, how does this tell us where the vertex is? Well, the vertex will be at the point where y is a minimum or maximum. Note: Completing the square and the quadratic formula are not the same method.įor more info on these methods, see the lessons at this link. This method is called completing the square because you create a perfect square trinomial, which factors into a binomial-squared.Ĥ) Quadratic formula. Specifically, it can be used for any quadratics in the form of "x^2 = a number" or "(ax+b)^2 = a number"ģ) Completing the square. This also only works for some quadratics. But, it is usually easier than other methods when it works.Ģ) Square root method. This does not work for all quadratics because not all are factorable. The 4 methods for solving are:ġ) Factoring. You are mixing up the name of the methods with the type of equations. Quadratic equations can be solved using 4 different methods. As to why they are called quadratics, see this link: Quadratic equations are any equation that can be written in the form: Ax^2 + Bx + C = 0, where A is not = 0.


 0 kommentar(er)
0 kommentar(er)
